線段的三等分點什麼意思

尺歸作圖不可能三等分角的。

在數學的歷史上有三個問題始終以可驚的力量堅廿了兩千多年。初等幾何學到現在至少已有了三千年的歷史，在這期間努力於初等幾何學之發展的學者們曾經遇到過很多的難題，而始終絞著學者腦汁的卻就是這三個問題。問題是「立方倍積」，「化圓為方」和「三等分角」，由於這三個問題的屹立不移，現在就被合稱為「三大問題」。

立方倍積

關於立方倍積的問題有一個神話流傳：當年希臘提洛斯（Delos）島上瘟疫流行，居民恐懼也向島上的守護神阿波羅（Apollo）祈禱，神廟裡的預言修女告訴他們神的指示：「把神殿前的正立方形祭壇加到二倍，瘟疫就可以停止。」由此可見這神是很喜歡數學的。居民得到了這個指示後非常高興，立刻動工做了一個新祭壇，使每一棱的長度都是舊祭壇棱長的二倍，但是瘟疫不但沒停止，反而更形猖獗，使他們都又驚奇又懼怕。結果被一個學者指出了錯誤：「棱二倍起來體積就成了八倍，神所要的是二倍而不是八倍。」大家都覺得這個說法很對，於是改在神前並擺了與舊祭壇同形狀同大小的兩個祭壇，可是瘟疫仍不見消滅。人們困擾地再去問神，這次神回答說：「你們所做的祭壇體積確是原來的二倍，但形狀卻並不是正方體了，我所希望的是體積二倍，而形狀仍是正方體。」居民們恍然大悟，就去找當時大學者柏拉圖（Plato）請教。由柏拉圖和他的弟子們熱心研究，但不曾得到解決，並且耗費了後代許多數學家們的腦汁。而由於這一個傳說，立方倍積問題也就被稱為提洛斯問題。

化圓為方

方圓的問題與提洛斯問題是同時代的，由希臘人開始研究。有名的阿基米得把這問題化成下述的形式：已知一圓的半徑是r，圓周就是2πr，面積是πr2。由此若能作一個直角三角形，其夾直角的兩邊長分別為已知圓的周長2πr及半徑r，則這三角形的面積就是

(1/2)(2πr)

什麼是三等分點

三等分點是把一條線段平均分成三等分的兩個點。

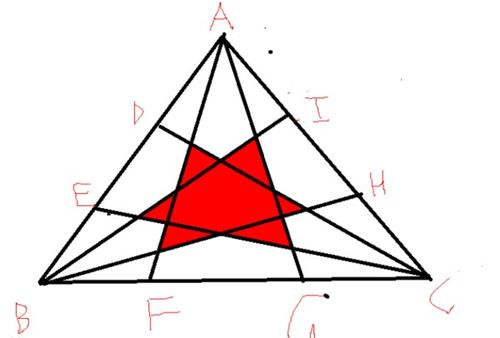
三等分點的作法有很多種，下面介紹四種三等分點的作法： 方法一： 現已知線段AB，要求作出AB的三等分點F,E。 步驟：做以AB為中線的三角形（方法如下：任意延長AB至點C，以B為圓心，截取HB=BC。

分別以H,C為圓心，HC為半徑畫弧，交HC垂直平分線於G,G1。連接AGG1，為三角形。）

做AG1垂直平分線，交AB於E，則EB=1/3AB。 E為圓心，BE半徑，畫圓與AB交於F。

E,F即是線段AB的三等分點。 方法二： 已知AB線段，做AB為底的等邊三角形，做AB的垂直平分線，設上面一點是C，再做BC的垂直平分線，兩平分線相交D吧，設AB中點為E，那麼DE是EC的三分之一，延長CE，然後取EF等於ED，可以看出三角形ADF是等邊三角形，做AD的垂直平分線，交AE於一點，設為G,AG就是AB的三分之一，如上做另一邊的三分之一，即可。

方法三： 把已知線段的一個端點作為頂點，任意作延長線，在延長線上從頂點開始任意截取相等的連續的三段，形成另一條線段，然後把已知線與你作的線段的另一個端點相連，形成三角形，過三等分點做底邊的平行線，交已知線段上的點就是所要的三等分點. 方法四： 已知線段AB，將AB線段四等分，分別為A,C,D,E,B。以ACD為直徑畫圓，再以CDEB為直徑畫圓，兩圓交點為點F，過F點作AB的垂線交AB於點F，點F即為線段AB的三等分點。